Sistem Teorisi: Durum Matrisi Ödev Soruları
Table of Contents
Problemler
Problem 1
\(\frac{d}{dt}x(t)=Ax(t)\) denklem sisteminin çözümünde özdeğerlerden 2 tanesi kompleks eşlenik kök, diğerleri reeldir. Kompleks özdeğerlere ilişkin özvektörler için
\begin{align*}e_1=e_1'+je_2''\end{align*} \begin{align*}e_2=\overline{e_1}=e_1'-je_1''\end{align*} \begin{align*}e_1'=\frac{1}{2}(e_1+\overline{e_1})\qquad e_1''=\frac{1}{2j}(e_1-\overline{e_1})\end{align*}eşitlikleri geçerli ise \(x_0=e_1''\) ilk koşulu için çözümünü özdeğerlere bağlı olarak elde ediniz.
Problem 2
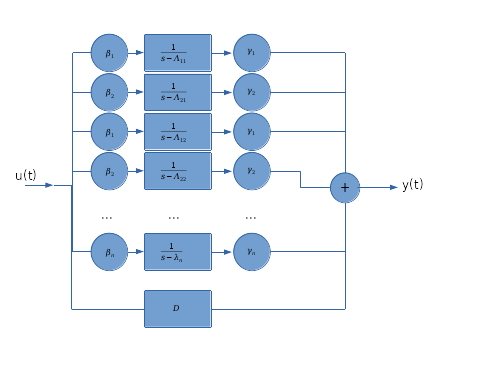
denklemleriyle verilen sistemde 4 özdeğer kompleks eşlenik ve diğerleri reel köklerdir. Bu sisteme ilişkin blok diyagramını çiziniz. \clearpage
Çözümler
Problem 1'in Çözümü
Çözümde kullanılacak kompleks eşlenik olan özdeğerleri \(\lambda_1=\alpha_1+jw_1\) ve \(\lambda_1=\alpha_1-jw_1\) olsun.
İlk koşul ifadesi
\(x_0=e_1''\) olarak soruda verilmiş ilk koşul ifadesi ilk kompleks özdeğerin imajiner kısmını gösterdiği için şu şekilde yazılabilir:
\begin{align*}x_0=e_1''=\frac{1}{2j}(e_1-\overline{e_1})\end{align*}Öz çözümün oluşturulması
Özdeğerleri kullanarak denklem sisteminin çözümüne giden yolda öz çözüm formülü uygulanır:
\begin{align*}x(t)=\sum^{n}_{i=1}e^{{\lambda_i}t}\xi_i(0)e_i=\frac{1}{2j}e^{{\lambda_1}t}e_1-\frac{1}{2j}e^{{\lambda_2}t}e_2\end{align*}Bu denklemde, \(e_2=\overline{e_1}\) olduğu göz önüne alınıp özdeğer ve özvektörler yerine koyulursa,
\begin{align*}x(t)=\frac{1}{2j}=[e^{\alpha_1 t}e^{jw_1 t}(e_1'+je_1'')-e^{\alpha_1 t}e^{-jw_1 t}(e_1'-je_1'')]\end{align*}Birkaç düzenleme sonrasında aşağıdaki denklem elde edilir:
\begin{align}x(t)=\frac{1}{2}e^{\alpha_1 t}[-j(e^{jw_1 t}-e^{-jw_1 t})e_1'+(e^{jw_1 t}+e^{-jw_1 t})e_1'']\end{align}Final
1 numaralı denkleme \(e^{jwt}=cos(wt)+j*sin(wt)\) dönüşümü uygulandığında
\begin{align*}x(t)=e^{\alpha_1 t}[sin(w_1 t)e_1'+cos(w_1 t)e_1'']\end{align*}şeklinde çözüm bulunur.
Problem 2'nin Çözümü
Matris dönüşümü
Öncelikle x(t) matrisi, özdeğerleri ve özvektörleri biçiminde yazılır. \(x(t)=Pz(t)\) şeklinde kapalı olarak ifade edilebilecek aşağıdaki dönüşüm uygulanır:
\begin{align*}\begin{bmatrix}x_1(t)\\x_2(t)\\...\\x_n(t)\end{bmatrix}=\begin{bmatrix}\frac{1}{2}(e_1+\overline{e_1})&\frac{1}{2j}(e_1-\overline{e_1})&\frac{1}{2}(e_3+\overline{e_3})&\frac{1}{2j}(e_3-\overline{e_3})&...&e_n\end{bmatrix}\begin{bmatrix}z_1(t)\\z_2(t)\\...\\z_n(t)\end{bmatrix}\end{align*}Sistem denkleminin yeniden yazılması
\(x(t)=Pz(t)\) dönüşümü yapıldığında sistem denklemi,
\begin{align*}\dot{z}(t)=P^{-1}APz(t)+P^{-1}Bu(t)\end{align*} \begin{align*}y(t)=CPz(t)+Du(t)\end{align*}şeklinde olacaktır. Buradaki \(AP\) matrisini gösterimi,
\begin{align*}AP=\begin{bmatrix}\frac{1}{2}(Ae_1+A\overline{e_1}) & \frac{1}{2j}(Ae_1-A\overline{e_1}) & \frac{1}{2}(Ae_3+A\overline{e_3}) & \frac{1}{2j}(Ae_3-A\overline{e_3}) & ... & Ae_n\end{bmatrix}\end{align*}Matrisin özvektörü ile çarpımıyla, özdeğerinin özvektörü ile çarpımı eşit olacağından \(Ae=\lambda e\) şeklide denklem düzenlenirse
\begin{align*}AP=\begin{bmatrix}\frac{1}{2}(\lambda_1 e_1+\overline{\lambda_1}\overline{e_1}) & \frac{1}{2j}(\lambda_1 e_1-\overline{\lambda_1}\overline{e_1}) & \frac{1}{2}(\lambda_3 e_3+\overline{\lambda_3}\overline{e_3}) & \frac{1}{2j}(\lambda_3 e_3-\overline{\lambda_3}\overline{e_3}) & ... & \lambda_n e_n\end{bmatrix}\end{align*}elde edilir ve \(\lambda\) değerleri \(\lambda=\alpha+jw\) şeklinde açılıp düzenlendiğinde elde edilen matris:
\begin{align*}AP=\begin{bmatrix}(\alpha_1e_1'-w_1e_1'') & (w_1e_1'+ \alpha_1e_1'') & (\alpha_3e_3'-w_3e_3'') & (w_3e_3'+\alpha_3e_3'') & ... & \lambda_n e_n\end{bmatrix}\end{align*}Elde edilen bu matrisi P matrisinin bir λ I matrisine benzer bir matris (Λ) ile çarpımı olarak düşünülebilir. Söz konusu matrisin köşegenindeki lambda değerlerine uymayan değerleri kaynağı kompleks kökler olacaktır.
\begin{align*}AP=\begin{bmatrix}e_1' & e_1'' & e_3' & e_3'' & ... & e_n\end{bmatrix}\begin{bmatrix}\alpha_1 & w_1 & 0 & 0 & ... & 0 \\ -w_1 & \alpha_1 & 0 & 0 & ... & 0 \\ 0 & 0 & \alpha_3 & w_3 & ... & 0 \\ 0 & 0 & -w_3 & \alpha_3 & ... & 0 \\ ... & ... & ... & ... & ... & 0 & \\ 0&0&0&0&0& \lambda_n \end{bmatrix}\end{align*}Bu çarpım AP=PΛ' olarak gösterilsin, bu durumda sistem denklemi tekrar düzenlenirse:
\begin{align*}\dot{z}(t)=\Lambda' z(t)+P^{-1}Bu(t)\end{align*} \begin{align*}y(t)=CPz(t)+Du(t)\end{align*}elde edilir ve bu eşitliklere Laplace dönüşümü uygulandığında
\begin{align}s\hat{z}(s)=\Lambda' \hat{z}(s)+P^{-1}B\hat{u}(s)\end{align} \begin{align}\hat{y}(s)=CP\hat{z}(s)+D\hat{u}(s)\end{align}elde edilir. 2 numaralı eşitlikteki \(\hat{z}(s)\) yalnız bırakılıp 3 numaralı eşitlikte yerine koyulduğunda aşağıdaki çözümü elde ederiz:
\begin{align*}\hat{y}(s)=C\frac{1}{s-\Lambda'}B\hat{u}(s)+D\hat{u}(s)\end{align*}\clearpage
Blok diyagramın oluşturulması
Elde edilen giriş çıkış ilişkisini blok diyagramında gösterebilmek için öncelikle matrislerin elemans boyutunda yapacağı işlemleri belirlememiz gerekir. B matrisi \(\beta\) elemanlarından ve C matrisi \(\gamma\) elemanlarından oluşsun. Bu durumda \(\Lambda'\) matrisinin elemanlarına göre olan blok aşağıdaki gibi olacaktır: